Chapter XI:

Properties of the Strong Nuclear Force,
Nuclear Properties of Bismuth,
and the Nuclear Gravitation Field Theory

The Nuclear Gravitation Field Theory states the “Strong Nuclear Force” is the same as Gravity.  Newton's Law of Gravity states that the gravitational attraction between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between the center of masses assuming the masses are uniform spheres or point sources of mass.  The Universal Gravitation Constant, “G,” has been assumed to be a universal constant ever since Isaac Newton established his Law of Gravity.  Newton's Law of Gravity is provided below:

Is the Universal Gravitation Constant really universal?  How bold and daring for anyone to challenge a physics principle that has been accepted for 500 years!  If the Strong Nuclear Force and Gravity are one and the same force, then the Universal Gravitation Constant cannot be a universal constant.  The Gravitation Constant will vary, somewhat, due to the number and arrangement of the protons and neutrons in the nucleus.  The “Binding Energy per Nucleon” for nucleons in the outermost ground state energy levels are different for each and every isotope of each element.  The “Binding Energy per Nucleon” for those specific outer nucleons is directly related to the field intensity of the Strong Nuclear Force in the vicinity of the nucleus, hence, the gravitational field of the nucleus.  For most relatively stable isotopes of most of the elements, the “Universal Gravitation Constant,” “G,” in Newton's Law of Gravity is a very good approximate value to use for determining the gravitational field at some given distance from a known mass.  Since Newton's Law of Gravity has been widely accepted for centuries, the expected Physics Community's response to any challenge to Newton’s Law of Gravity will be to state the observed behavior provides the exact justification why the Strong Nuclear Force and Gravity cannot be the same.  However, physical evidence exists that can support the Nuclear Gravitation Field Theory position.

Let's first look at Newton's Law of Gravity and the “Universal Gravitation Constant.”  The following passage was extracted from “Physics, Parts I and II,” by David Halliday and Robert Resnick, pages 348 to 349.  This passage discusses Lord Cavendish's Experiment designed to measure the Universal Gravitation Constant:

To determine the value of G it is necessary to measure the force of attraction between two known masses.  The first accurate measurement was made by Lord Cavendish in 1798.  Significant improvements were made by Poynting and Boys in the nineteenth century.  The present accepted value of G is 6.6726x10^-11 Newton-meter²/kg², accurate to about 0.0005x10^-11 Newton-meter²/kg².  In the British Engineering System this value is 3.436x10^-8 lb-ft²/slug².

The constant G can be determined by the maximum deflection method illustrated in Figure 11-1.  Two small balls, each of mass m, are attached to the ends of a light rod.  This rigid “dumbbell” is suspended, with its axis horizontal, by a fine vertical fiber.  Two large balls each of mass M are placed near the ends of the dumbbell on opposite sides.  When the large masses are in the positions A and B, the small masses are attracted, by the Law of Gravity, and a torque is exerted on the dumbbell rotating it counterclockwise, as viewed from above.  When the large masses are in the positions A' and B', the dumbbell rotates clockwise.  The fiber opposes these torques as it is twisted.  The angle through which the fiber is twisted when the balls are moved from one position to the other is measured by observing the deflection of a beam of light reflected from the small mirror attached to it.  If the values of each mass, the distances of the masses from one another, and the torsional constant of the fiber are known, then G can be calculated from the measured angle of twist.  The force of attraction is very small so that the fiber must have an extremely small torsion constant if a detectable twist in the fiber is to be measured.

The masses in the Cavendish balance of Figure 11-1 are, of course, not particles but extended objects.  Since each of the masses are uniform spheres, they act gravitationally as though all their mass were concentrated at their centers.

Because G is so small, the gravitational forces between bodies on the earth's surface are extremely small and can be neglected for ordinary purposes.

The Cavendish balance, used for experimental verification of Newton's Law of Universal Gravitation.  Masses m and m are suspended from a quartz fiber.  Masses M and M can rotate on a stationary support.  An image of the l amp filaments is reflected by the mirror attached to m and m onto the scale so that any rotation of m and m can be measured.

Figure 11-1:  The Cavendish Experiment

Reference:  “Physics, Parts I and II,” David Halliday and Robert Resnick

Lord Cavendish did not set out to prove the Universal Gravitation Constant, “G,” was, in fact, a universal constant by his experiment.  Lord Cavendish already assumed G to be a universal constant based on Newton's Law of Gravity, a physical law that had been accepted for over one hundred years by that time.  The Cavendish Experiment intent was to determine the value of G by measuring the torque on the quartz fiber resulting from the gravitational attraction of the two small masses to their respective large masses.  The measured torque is proportional to the force between the masses.  G can be calculated by rearranging the equation for Newton's Law of Gravity and then solving for G.

The material content of the masses used in the experiment was not mentioned because G was assumed to be universal.  Lord Cavendish used the G calculated from his experiment to determine the average density of the Earth.  Once again, his calculation was based upon the assumption that G is a universal constant.  Assuming G is a constant is acceptable because an average G is relatively accurate for use in astronomical calculations.  G doesn't vary significantly under most conditions where gravitational fields must be evaluated.  However, G is a function of the matter contained in the mass of interest.  There is no current method available to measure mass, directly.  A local gravitational field must be determined and the weight of a mass is measured to “determine the mass.”  This method for measuring mass requires assuming that G is a constant.

The Nuclear Gravitation Field Theory provides a solid case for demonstrating the “Strong Nuclear Force” and Gravity to be one and the same force.  I mentioned previously each individual nucleus will have a different gravitation constant consistent with the “Binding Energy per Nucleon” for the outermost ground state energy level nucleons which is directly related to the intensity of the “Strong Nuclear Force” just outside the nucleus.  Consider Element 83, Bismuth.  The only stable isotope of Bismuth has 83 protons (by definition) and has 126 neutrons, therefore, has an atomic mass of approximately 209.  Table 11-1, “Periodic Table of the Elements - p-Orbitals,” and Table 11-2, “Table of the Nuclides - Lead and Bismuth,” indicate the nuclear and chemical properties of Bismuth.

Table 11-1:  Periodic Table of the Elements - p-Orbitals

13	14	15	16	17	18
p-Orbitals
				1 H	2 He
5 B	6 C	7 N	8 O	9 F	10 Ne
13 Al	14 Si	15 P	16 S	17 Cl	18 Ar
31 Ga	32 Ge	33 As	34 Se	35 Br	36 Kr
49 In	50 Sn	51 Sb	52 Te	53 I	54 Xe
81 Tl	82 Pb	83 Bi	84 Po	85 As	86 Rn
113 UUT	114 UUQ	115 UUP	116 UUH	117 UUS	118 UUO

Reference:  http://www.webelements.com/index.html

Table 11-2:  Table of the Nuclides - Lead and Bismuth

85 At	At208	At209	At210	At211	At212	At213	At214
84 Po	Po207	Po208	Po209	Po210	Po211	Po212	Po213
83 Bi	Bi206	Bi207	Bi208	Bi209	Bi210	Bi211	Bi212
82 Pb	Pb205	Pb206	Pb207	Pb208	Pb209	Pb210	Pb211
81 Tl	Tl204	Tl205	Tl206	Tl207	Tl208	Tl209	Tl210
80 Hg	Hg203	Hg204	Hg205
Z ↑ N →	123	124	125	126	127	128	129

Reference:  http://www2.bnl.gov/CoN/nuchart10.html

In Chapter VII, “The Schrodinger Wave Equation and Quantum Mechanics -The Particle and Wave Characteristics of Matter,” the “proton magic number” and “neutron magic number” for the nucleus were introduced.  The “magic number” represents the number of protons or neutrons required to fill all ground state energy levels of a nucleus to capacity.  In Table 11-2, “Table of the Nuclides - Lead and Bismuth,” ₈₂Pb²⁰⁸ (Lead) has 82 protons and 126 neutrons in its nucleus and is considered to be “double magic” because it contains both a “proton magic number” of protons and a “neutron magic number” of neutrons in its nucleus.  ₈₃Bi²⁰⁹ (Bismuth) has 83 protons in its nucleus, therefore, its nucleus contains one proton beyond the “proton magic number” of 82.  That extra proton, number 83, must reside in the next proton energy level, the 7^th proton energy level, because the 6^th proton energy level is already filled to capacity.  ₈₃Bi²⁰⁹ contains the “neutron magic number” of 126 in its nucleus.  Bismuth is the highest number element known, thus far, that has a stable isotope in accordance with the Table of the Nuclides.  All higher number elements are radioactive and have a decay half-life.  Table 11-3, “Nucleon Energy Levels, Pb-208 and Bi-209,” provides the numbers of protons and neutrons that fill each energy level of the nucleus for ₈₂Pb²⁰⁸ (Lead) and ₈₃Bi²⁰⁹ (Bismuth).

Table 11-3:  Nucleon Energy Levels for Lead (Pb-208) and Bismuth (Bi-209)

Energy Level	1 (He)	2 (O)	3 (Ca)	4 (Ni)	5 (Sn)	6 (Pb)	7 (E114)	8 (?)	Total Protons and Neutrons
Protons Lead (82Pb208) Neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	32p 32n	44n		82p 126n
Protons Bismuth (83Bi209) Neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	32p 32n	1p 44n		83p 126n

Reference:  http://atom.kaeri.re.kr/ton/nuc11.html

NOTE:

The nuclear proton and neutron energy level tables in Table 11-3, “Nucleon Energy Levels for Lead (Pb-208) and Bismuth (Bi-209),”Table 11-4, “Nucleon Energy Levels for Element 114 and Element 115,” and Table 11-5, “Nucleon Energy Levels for Other Nuclei of Interest,” may be simplified representations of the actual nuclear energy levels filled for the protons and neutrons.  It is expected that proton and neutron energy levels may exist in the nucleus having a similar characteristic to the 3d, 4d, 4f, 5d, 5f, and 6d electron energy levels.  In Chapter VII, Figure 7-1, “The Order of Electron Fill of the Electron Energy Levels Around the Nucleus,” illustrates the order in which electrons fill electron energy levels.  Electron energy level 3d begins to fill after electron energy level 4s is filled but prior to filling electron energy level 4p.  Electron energy level 4d begins to fill after electron energy level 5s is filled but prior to filling electron energy level 5p.  Electron energy levels 4f and 5d begin to fill after electron energy level 6s is filled but prior to filling electron energy level 6p.  Electron energy levels 5f and 6d begin to fill after electron energy level 7s is filled but prior to filling electron energy level 7p.  The 4th nuclear proton and neutron energy levels and higher, as designated in the tables, may include lower nuclear proton and neutron energy levels that are filled in like manner to the 3d, 4d, 4f, 5d, 5f, and 6d electron energy levels.  For example, a full 5th nuclear proton or neutron energy level may include filling a “4d” nuclear energy level to make up the total number of either 22 protons or 22 neutrons as indicated by the tables.

If the energy levels in the nucleus have a similar characteristic to those of the electrons, it would be expected that a lone proton in the outermost ground state energy level of a nucleus, such as Bismuth-209, would be “loosely bound” in a similar manner to a lone electron in the outermost ground state energy level of an atom such as Sodium.  The atomic radius of the neutral Sodium atom, Element 11, is 2.23 Angstroms.  Sodium has an electron configuration of 1s²2s²2p⁶3s¹.  The atomic radius for Neon, Element 10, a noble gas with a full outer electron energy level, is 0.51 Angstroms.  Neon has an electron configuration of 1s²2s²2p⁶.  The atomic radius for Argon, Element 18, another noble gas with a full outer electron energy level, is 0.88 Angstroms.  Argon has an electron configuration of 1s²2s²2p⁶3s²3p⁶.

Reference:  http://chemlab.pc.maricopa.edu/periodic/periodic.html.

Neon represents the noble gas just below Sodium in atomic number on the Periodic Table and Argon represents the noble gas just above Sodium in atomic number on the Periodic Table.

The radius of Sodium is 4.37 times larger than the radius for Neon and is 2.53 times larger than the radius for Argon.  Neon's outer electron ground state energy level is level 2.  Sodium's and Argon's outer electron ground state energy level is level 3.  The relatively large atomic radius for Sodium indicates the rather weak hold the Sodium nucleus has on the “lone electron” in the 3^rd electron energy level.  The nuclear characteristics of Bismuth, Element 83, are expected to be analogous to Sodium's electronic characteristics because Bismuth's 83^rd proton is a “lone proton” in the 7^th nuclear proton energy level.

The Nuclear Gravitation Field Theory states the “Strong Nuclear Force” and Gravity are one and the same force.  Assuming that the “Strong Nuclear Force” and Gravity are the same, nuclides having the greatest “Strong Nuclear Force” intensity near the surface of the nucleus will experience the greatest amount of “Space-Time Compression” in the vicinity of the nucleus.  The “Strong Nuclear Force” intensity will “drop off” very rapidly and its field strength will be very feeble outside the associated atom of these Nuclides.  Nuclides that fall into this category include ₂He⁴ (Helium), ₈O¹⁶ (Oxygen), ₂₀Ca⁴⁰ (Calcium), and ₈₂Pb²⁰⁸ (Lead) because each of these each nuclei contains both a proton and a neutron magic number and are considered “double magic.”  Nuclides having the least “Strong Nuclear Force” intensity near the surface of the nucleus will experience the smallest amount of “Space-Time Compression.”  Hence, the “Strong Nuclear Force” intensity will “drop off” more gradually and the field strength of the “Strong Nuclear Force” will be more intense outside the associated atom of these nuclides.  ₈₃Bi²⁰⁹ (Bismuth) falls into this category because the Bismuth nucleus contains a “loose-bound” proton in the 7^th nuclear proton energy level.  The Bismuth atom does not become “larger” because of the reduced “Space-Time Compression.”  As discussed previously in Chapter VIII, the wavelength of the Nuclear Electric Field produced by the protons in the nucleus determines the positions of the electron orbitals around the nucleus and, hence, the size of the atom -- equivalent to the size of the electron cloud surrounding the nucleus.  The Nuclear Electric Field intensity is a function of the “virtual distance,” or “Compressed Space-Time” distance, from the nucleus.  The “virtual distance” is the “apparent measured distance” from the nucleus based upon the “Space-Time Compression” that takes place in the strong quantized Nuclear Gravitation Field, or “Strong Nuclear Force,” in the vicinity of the nucleus.  If one could “stretch” the “Compressed Space-Time” distance into its equivalent “Normal Space-Time” distance, the electron orbitals would appear to be located significantly farther from the nucleus.

Let's perform a comparison of the Nuclear Gravitation Fields and Nuclear Electric Fields of the stable “double-magic” nucleus of Lead-208, ₈₂Pb²⁰⁸, and the stable nucleus of Bismuth-209, ₈₃Bi²⁰⁹, which contains a lone proton in its outer (7^th) proton energy level.  The Bismuth-209 nucleus has a Nuclear Gravitation Field at its nuclear surface that is significantly weaker than the Nuclear Gravitation Field of the Lead-208 nucleus at its nuclear surface.  The amount of “Compressed Space-Time” occurring in the vicinity of the Bismuth nucleus is reduced in comparison to the Lead nucleus.  The “virtual distance” of the electron orbitals from the Bismuth-209 nucleus will be similar to the “virtual distance” of the electron orbitals for the Lead-208 nucleus. . The electron orbitals for Bismuth-209 will be a bit closer because its Nuclear Electric Field is slightly more intense than that of Lead-208.  The Bismuth-209 nucleus contains 83 protons, whereas, the Lead-208 nucleus contains 82 protons.  For this exercise, let's assume the electron orbital “virtual distances” are equivalent.  Since the Nuclear Gravitation Field intensity for Bismuth-209 at its nuclear surface is lower than the Nuclear Gravitation Field intensity for Lead-208 at its nuclear surface, the amount of “Space-Time Compression” in the vicinity of the Bismuth-209 nucleus is reduced compared to the Lead-208 nucleus.  Since the Bismuth-209 Nuclear Gravitation Field “drops off” more gradually than the Lead-208 Nuclear Gravitation Field, the “Compressed Space-Time” distance, or “virtual distance” is closer to the “actual distance” from the nucleus for Bismuth-209 than for Lead-208.  The Nuclear Electric Field intensity is a function of the “Compressed Space-Time” distance from the nucleus.  The Nuclear Gravitation Field intensity is a function of the “Normal Space-Time” distance from the nucleus.  Therefore, the electron orbitals for the Bismuth-209 nucleus will be closer to the nucleus based upon “actual distance” because their orbitals are a function of the Nuclear Electric Field that propagates based upon “Compressed Space-Time.”  The Bismuth-209 nuclear “Compressed Space-Time” distance is closer to its “Normal Space-Time” distance than the Lead-208 nuclear “Compressed Space-Time” distance is to its “Normal Space-Time” distance.  The electron orbitals occur in a stronger Nuclear Gravitation Field for the Bismuth-209 nucleus than for the Lead-208 nucleus.  The Nuclear Gravitation Field outside the electron cloud for the Bismuth-209 atom is stronger than the Nuclear Gravitation Field outside the electron cloud for the Lead-208 atom.

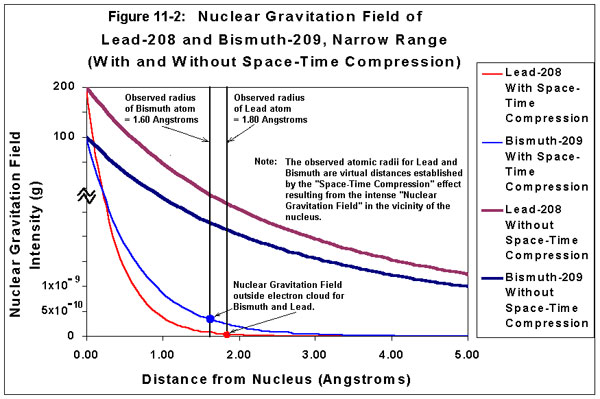
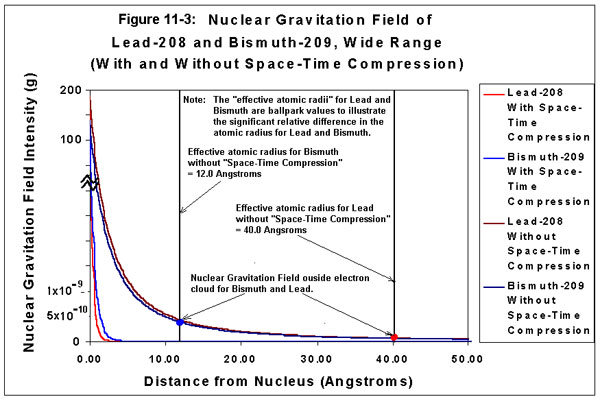
Figure 11-2, “Nuclear Gravitation Field of Lead-208 and Bismuth-209, Narrow Range,” provides a graphical representation of the Nuclear Gravitation Fields of Lead-208 and Bismuth-209 with and without “Space-Time Compression” effects.  Figure 11-2 illustrates the “virtual distance,” or “relative distance,” from the nucleus to the end of the electron cloud for Lead-208 and Bismuth-209 as observed with “Space-Time Compression” effects in the vicinity of the nucleus of each atom.  Note the Nuclear Gravitation Field intensity for Bismuth-209 is significantly greater at the end of its electron cloud relative to the Nuclear Gravitation Field intensity of Lead-208 at the end of its electron cloud.  Figure 11-3, “Nuclear Gravitation Field of Lead-208 and Bismuth-209, Wide Range,” also provides a graphical representation of the Nuclear Gravitation Fields of Lead-208 and Bismuth-209 with and without “Space-Time Compression” effects.  Figure 11-3 illustrates the “actual distance,” or “effective distance,” from the nucleus to the end of the electron cloud for Lead-208 and Bismuth-209 if “Space-Time Compression” effects were not present.  Note the “actual distance,” or “effective distance,” of the end of the electron cloud from the nucleus for Lead-208 is significantly greater than the “actual distance,” or “effective distance” of the end of the electron cloud from the nucleus for Bismuth-209.

Figure 11-2:  Nuclear Gravitation Field of Lead-208 and Bismuth-209
Narrow Range

Figure 11-3:  Nuclear Gravitation Field of Lead-208 and Bismuth-209
Wide Range

NOTE 1:	Figure 11-2 and Figure 11-3 only provide “ballpark” values for the “Nuclear Gravitation Field Intensity” of Lead-208 and Bismuth-209 in units of “g-force” as a function of distance from the nucleus.  In order to calculate exact values for the Nuclear Gravitation Field intensity, a very sophisticated computer program must be used to perform the iterative calculation required with the Schrodinger Wave Equation to include the effects of General Relativity (i.e., “Space-Time Compression”) with Quantum Mechanics.  The intent of the graphs is only to provide a relative visual representation of the Nuclear Gravitation Field as a function of distance from the nucleus.  The Nuclear Gravitation Field intensity curves for Lead-208 and Bismuth-209 “without Space-Time Compression” are proportional to a 1/r2 function where r is the radial distance from the nucleus.  The curves accounting for “Space-Time Compression” have a correction factor for the Nuclear Gravitation Field intensity as a function of distance, which is a function of the Nuclear Gravitation Field intensity.  The distance from the nucleus is, therefore, compressed.  The Nuclear Gravitation Field intensity at the nuclear surface is on the order of 10 billion times to 100 billion times greater than the Nuclear Gravitation Field intensity in the proximity of the end of the electron cloud, which represents the atomic radius.  Neither a purely logarithmic nor a purely linear scale would be practical for indicating the relative Nuclear Gravitation Field strength as a function of distance from the nucleus of the atom.  The vertical scale depicting “Nuclear Gravitation Field Intensity” is quasi-linear at the bottom the graph near the origin, becomes logarithmic as it moves away from the origin, and then becomes quasi-linear at the top of the graph.
NOTE 2:	The difference in the Nuclear Gravitation Field Intensity between 82Pb208 and 83Bi209 is grossly exaggerated in order to illustrate how reducing the intensity of the Nuclear Gravitation Field in the vicinity of the nucleus of an atom will produce a greater intensity gravity field at the outside of the electron cloud of that atom.  If Bismuth had such a large gravitational attraction outside its electron cloud relative to Lead, spheres of Bismuth would fall about 10 times faster than Lead.  In actuality, the gravitational field of Bismuth outside its electron cloud is only a small percentage greater than the gravitational field of Lead outside its electron cloud.

The following referenced information discusses the observed scientific evidence supporting the Nuclear Gravitation Field Theory.  The observed gravitational characteristics of Bismuth demonstrate the “Strong Nuclear Force” and Gravity are one and the same.

RS Electrogravitic References:  Part 7 of 19

When individual molecules are not permanently magnetized, it is possible in some cases to have a relative magnetic permeability, μ, which is less than one.  Such a material, like hydrogen or BISMUTH, is called diamagnetic.  It tends to expel magnetic field, and is repelled from regions of stronger magnetic field.  The names paramagnetic and diamagnetic are sometimes confused.  Paramagnetic is analogous to a dielectric in an electric field, while diamagnetic is quite the opposite.  It is not possible to give a simple argument of why diamagnetism can occur.  It is strictly speaking a quantum effect.  However, one can see that there might be diamagnetic tendencies if electric currents can flow within molecules.  An increasing magnetic field always tends to induce currents to flow in such a way as to tend to prevent the increase in the field.  This is (at least temporarily) a diamagnetic kind of effect.  Thus the case where the relative magnetic permeability, μ < 1, is connected with the flow of electric charges in a magnetic field.  There is no analogous case with electric fields since isolated magnetic poles do not, so far as is known, exist.

--  “The New Physics” edited by Paul Davies

GE engineer Henry William Wallace found unusual gravitational affects in spinning odd atomic nuclide metals.  Odd atomic nuclide metals are those in which the sum of the protons are not equal to the number of neutrons, i.e., more neutrons.  See U.S. Patents 3,626,605 and 3,626,606.

--  Ron Kita

Reference: http://www.padrak.com/ine/RS_REF7.html

“Since the dynamic interaction field arising through gravitational coupling is a function of both the mass and proximity of two relatively moving bodies, then the resultant force field is predictably maximized within the nucleus of an atom due to the relatively high densities of the nucleons plus the fact that the nucleons possess both intrinsic and orbital components of angular momentum.  Such force fields may, in fact, account for a significant portion of the nuclear binding force found in all of nature.”

References:	United States Patent Number 3,626,605, “Method and Apparatus for Generating a Secondary Gravitational Force Field”
	United States Patent Number 3,626,606, “Method and Apparatus for Generating a Dynamic Force Field”

“Also indicated in the embodiment of FIGURES 7A* and 7B* is the orientation of the flux within the mass circuit, the latter being constructed preferredly of BISMUTH.”

Reference:

United States Patent Number 3,626,605, “Method and Apparatus for Generating a Secondary Gravitational Force Field”

NOTE:

FIGURES 7A* and 7B* mentioned in the text are illustrations included with Henry William Wallace's description of his invention - the machine designed to generate a secondary gravitational force field - within the U.S. Patent Number 3,626,605 document.

--  Henry William Wallace

Reference:

United States Patent Number 3,626,605, “Method and Apparatus for Generating a Secondary Gravitational Force Field”

Bismuth is also mentioned in the literature as being electrogravitic.  Spinning discs of Bismuth (patented by GE Engineer Henry William Wallace:  U.S. Patent #3,626,605, U.S. Patent #3,626,606, and U.S. Patent #3,823,570) have apparently been shown to DEFY GRAVITY.  Bismuth, with a strong positive electrostatic charge applied to it, has also been shown to actually lose weight, right down to ZERO.  Spheres of Bismuth, when dropped, have reportedly fallen faster than they are supposed to (according to Newton's Law of Gravity).

Reference:  http://erntheburn.tripod.com/115thelement/ArtBell.htm

Bismuth spheres falling faster than predicted by Newton's Law of Gravity, Henry William Wallace's speculation of a possible connection between the force of Gravity and the “Strong Nuclear Force,” and rotating Bismuth discs generating secondary gravitational force fields provide the evidence the “Strong Nuclear Force” and Gravity are one and the same.  Since the “Strong Nuclear Force” is weaker in Bismuth because of the “lone 83^rd proton” in the 7^th nuclear proton energy level, less “Space-Time Compression” takes place in the vicinity of the ₈₃Bi²⁰⁹ nucleus.  The intensity of the “Strong Nuclear Force” extending outside the Bismuth atom is significant enough to provide a measurable gravitational attraction with greater intensity than predicted by Newton's Law of Gravitation.  Two separate gravitation constants exist that are associated with the nucleus.  The first gravitation constant is directly related to the Nuclear Gravitation Field at the surface of the nucleus.  This constant is directly related to the “Binding Energy per Nucleon” for the nucleons in the outermost ground state nuclear energy levels and the “Strong Nuclear Force” intensity at the surface of the nucleus.  The second gravitation constant, which has been the assumed “Universal Gravitation Constant,” “G,” is the constant associated with the gravitational field propagating outside the atom.  This second constant actually varies from isotope and element to isotope and element based upon the “Binding Energy per Nucleon” for the outermost ground state energy levels in the nucleus.  The first and second gravitation constants are quasi-inversely proportional because of the General Relativistic effects of “Space-Time Compression” in the vicinity of the nucleus.

Physicists have believed that there may be an island of stability in the vicinity of Element 114 (UnUnQuadium or UUQ) in a sea of instability for the “superheavy elements” in the Table of the Nuclides.  114 protons is a proton magic number.  It is very possible that an isotope of Element 114 containing a neutron magic number of 184 neutrons could exist as a stable isotope.  This Element 114 isotope would be “double magic” in like manner to ₈₂Pb²⁰⁸.  An isotope of Element 114 with 175 neutrons (₁₁₄UUQ²⁸⁹) has been identified by the Lawrence-Berkeley Laboratories having a half-life of 30 seconds (Reference: “Pushing the Limits of the Periodic Table,” Gina Stafford, The Knoxville News-Sentinel).  A 30-second half-life doesn't seem to be a significant period of time.  However, 30 seconds is a relative eternity compared to the half-lives of the elements between Element 100 and Element 109, which are on the order of milliseconds to microseconds.

The nuclear reaction producing the Element 114 isotope ₁₁₄UUQ²⁸⁹ containing 175 neutrons with a 30 second half-life is provided below:

₉₄Pu²⁴⁴  +  ₂₀Ca⁴⁸   →   ₁₁₄UUQ²⁸⁹  +  3₀n¹

The nuclear reaction producing the Element 114 isotope ₁₁₄UUQ²⁸⁸ containing 174 neutrons with a half-life of 2 seconds is provided below:

₉₄Pu²⁴⁴  +  ₂₀Ca⁴⁸   →   ₁₁₄UUQ²⁸⁸  +  4₀n¹

The Element 114 isotope ₁₁₄UUQ²⁸⁵ containing 171 neutrons was identified as one of the intermediate product elements in a decay chain after an isotope of Element 118 (UnUnOctium or UUO), ₁₁₈UUO²⁹³, was produced by the following nuclear reaction:

₈₂Pb²⁰⁸  +  ₃₆Kr⁸⁶   →   ₁₁₈UUO²⁹³  +  ₀n¹

This Element 118 (UnUnOctium or UUO) isotope, ₁₁₈UUO²⁹³, alpha decayed (alpha decay is a nuclear decay process that liberates a Helium nucleus, ₂He⁴, from the parent nucleus) to become Element 116 (UnUnHexium or UUH) isotope ₁₁₆UUH²⁸⁹ in 12 milliseconds.  The Element 116 isotope, ₁₁₆UUH²⁸⁹, alpha decayed to become Element 114 isotope, ₁₁₄UUQ²⁸⁵ in 0.60 milliseconds.  This Element 114 isotope, ₁₁₄UUQ²⁸⁵, existed for only 0.58 milliseconds before alpha decaying to become Element 112 (UnUnBium or UUB) isotope ₁₁₂UUB²⁸¹.  The alpha decay process continued until “the final product of the decay chain,” an isotope of an element that was “relatively stable,” was obtained.

Reference:  http://www.webelements.com/webelements/elements/text/Uuq/key.html

The next neutron magic number beyond 126 is 184.  The Element 114 isotope containing 175 neutrons has a relatively long half-life for a nucleus short of 9 neutrons in its 8^th neutron energy level.  Assuming 184 is the next magic number for neutrons, a stable isotope of Element 114 containing 184 neutrons, designated ₁₁₄UUQ²⁹⁸, could exist and would be expected to have an atomic mass of approximately 298 Atomic Mass Units (AMU).  The probability of a stable “double magic” isotope of Element 114, ₁₁₄UUQ²⁹⁸, appears to be quite high considering the 0.58 millisecond life of the isotope ₁₁₄UUQ²⁸⁵, which is short 13 neutrons from the “double magic” nuclear configuration, the 2 second half-life of isotope ₁₁₄UUQ²⁸⁸, which is short 10 neutrons from the “double magic” nuclear configuration, and the 30 second half-life of the isotope ₁₁₄UUQ²⁸⁹, which is short 9 neutrons from the “double magic” nuclear configuration.  The half-lives of the Element 114 isotopes are rising very significantly as the number of neutrons in the Element 114 isotopes approaches the neutron magic number of 184.

Likewise, there may be a stable isotope of Element 115 (UnUnPentium or UUP), a “proton magic number plus one” element, containing a neutron magic number of 184 similar in nuclear configuration to ₈₃Bi²⁰⁹.  This isotope of Element 115 (UnUnPentium or UUP) would have an atomic mass of approximately 299 AMU and would be designated ₁₁₅UUP²⁹⁹.  Element 115 is expected to be approximately 1.43 times more massive than Bismuth and would have a smaller “Binding Energy per Nucleon” for the nucleons in the outer ground state energy levels than Bismuth.  Therefore, Element 115 should have a greater gravitational field outside the atom than Bismuth.  This isotope of Element 115, if it is either discovered or synthesized, should provide gravitational properties exceeding that of ₈₃Bi²⁰⁹.  Table 11-4, “Nucleon Energy Levels for Element 114 and Element 115,” provides the numbers of protons and neutrons that fill each energy level of the nucleus for ₁₁₄UUQ²⁹⁸ and ₁₁₅UUP²⁹⁹.

Table 11-4:  Nucleon Energy Levels for Element 114 and Element 115

Energy Level	1 (He)	2 (O)	3 (Ca)	4 (Ni)	5 (Sn)	6 (Pb)	7 (E114)	8 (?)	Total Protons and Neutrons
Protons E114 (114UUQ298) Neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	32p 32n	32p 44n	58n	114p 184n
Protons E115 (115UUP299) Neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	32p 32n	32p 44n	1p 58n	115p 184n

Table 11-5:  Nucleon Energy Levels for Other Nuclei of Interest

Energy Level	1 (He)	2 (O)	3 (Ca)	4 (Ni)	5 (Sn)	6 (Pb)	Total Protons and Neutrons
protons Helium (2He4) neutrons	2p 2n						2p 2n
protons Lithium (3Li7(6)) neutrons	2p 2n	1p 2n (1n)					3p (3n) 4n
protons Oxygen (8O16) neutrons	2p 2n	6p 6n					8p 8n
protons Fluorine (9F19) neutrons	2p 2n	6p 6n	1p 2n				9p 10n
protons Calcium (20Ca40) neutrons	2p 2n	6p 6n	12p 12n				20p 20n
protons Scandium (21Sc45) neutrons	2p 2n	6p 6n	12p 12n	1p 4n			21p 24n
protons Nickel (28Ni58(60)) neutrons	2p 2n	6p 6n	12p 12n	(12n) 10n			28p (32n) 30n
protons Copper (29Cu63(65)) neutrons	2p 2n	6p 6n	12p 12n	8p 8n	1p (8n) 6n		29p (36n) 34n
protons Tin (50Sn120(118) 50Sn((116))) neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	((16n)) (18n) 20n	50p ((66n)) (68n) 70n
protons Antimony (51Sb121(123)) neutrons	2p 2n	6p 6n	12p 12n	8p 8n	22p 22n	1p (22n) 20n	51p (72n) 70n

References:  http://atom.kaeri.re.kr/ton/nuc1.html, http://atom.kaeri.re.kr/ton/nuc3.html and, http://atom.kaeri.re.kr/ton/nuc6.html

The proton magic numbers and their associated elements, as indicated in Table 11-3, “Nucleon Energy Levels for Lead (Pb-208) and Bismuth (Bi-209),” Table 11-4, “Nucleon Energy Levels for Element 114 and Element 115,” and Table 11-5, “Nucleon Energy Levels for Other Nuclei of Interest,” are 2 for Helium, 8 for Oxygen, 20 for Calcium, 28 for Nickel, 50 for Tin, 82 for Lead, and 114 for UUQ.  The most abundant isotopes of Helium, Oxygen, and Calcium are ₂He⁴, ₈O¹⁶, and ₂₀Ca⁴⁰.  All these isotopes are “double magic.”  Could other stable isotopes of elements containing a “proton magic number plus one” and containing a neutron magic number similar to Bismuth exist?  The other elements that are “proton magic number plus one” are Lithium (Element 3), Fluorine (Element 9), Scandium (Element 21), Copper (Element 29), and Antimony (Element 51).  Table 11-5 provides the logic of nuclear energy level fill for both the “proton magic number” elements and the “proton magic number plus one” elements.  The most stable isotopes of Lithium, Fluorine, Scandium, Copper, and Antimony do not contain neutron magic numbers. 93% of Lithium is ₃Li⁷, which contains 2 neutrons in the 3^rd (outer ground state) neutron energy level.  7% of Lithium is ₃Li⁶, which contains only one extra neutron in the 3^rd neutron energy level.  Lithium has a rather small atomic mass so its overall contribution to a gravitational field would be small.  Lithium is a very reactive alkali metal and is rather hazardous to work with for performing gravitational anomaly measurements.  Fluorine, ₉F¹⁹, contains 2 neutrons in the 3^rd (outer ground state) neutron energy level.  Fluorine has a rather small atomic mass so its overall contribution to a gravitational field would be small.  Fluorine is a halogen gas at room temperature and is difficult and hazardous to work with for performing gravitational anomaly measurements.  Scandium, ₂₁Sc⁴⁵, contains 4 neutrons in the 4^th (outer ground state) neutron energy level.  The two most abundant isotopes of Copper, ₂₉Cu⁶³ and ₂₉Cu⁶⁵, contain 6 or 8 neutrons, respectively, in the 5^th (outer ground state) neutron energy level.  The two most abundant isotopes of Antimony, ₅₁Sb¹²¹ and ₅₁Sb¹²³, contain 20 or 22 neutrons, respectively, in the 6^th (outer ground state) neutron energy level.  Antimony's 6^th neutron energy level contains about 2/3 full capacity of neutrons because the 6^th neutron energy level holds 32 neutrons.  Each of these “proton magic number plus one” element isotopes have additional neutrons in unfilled outer ground state energy levels.  The nuclear binding of the lone proton in the outer ground state proton energy level is expected to be stronger than ₈₃Bi²⁰⁹ (Bismuth) because of the additional neutrons in unfilled energy levels.  A “Strong Nuclear Force” (Nuclear Gravitation Field) with a very intense field at the surface of the nucleus will result in a greater amount of Space-Time Compression in the vicinity of the nucleus.  The intensity of the “Strong Nuclear Force” propagating outside the atom of these elements would not be expected to be as significant as Bismuth (₈₃Bi²⁰⁹).  However, these “proton magic number plus one” elements require further study to determine if they display any unusual gravitational characteristics.

It appears that ₈₃Bi²⁰⁹ is a very unique element isotope.  ₈₃Bi²⁰⁹ has a relatively large atomic mass and is the only stable isotope of Bismuth, the highest number element currently officially known to man to be stable.  ₈₃Bi²⁰⁹ is a “proton magic number plus one” element that contains a neutron magic number.  ₈₃Bi²⁰⁹ displays gravitational characteristics unlike any other known element.  Should a stable or long half-life isotope of Element 115, a “would be” “proton magic number plus one” element containing a “neutron magic number,” ever be discovered or synthesized, it should be interesting to study the gravitational characteristics of that isotope of Element 115 and compare it to Bismuth (₈₃Bi²⁰⁹).

The General Relativistic characteristics of the nucleus and “Space-Time Compression” altering the Nuclear Gravitation Field intensity applies to another observed phenomenon associated with the nucleus.  When physicists attempt to “pull” a nucleus apart, they have reported that the Strong Nuclear Force seems to get much stronger.  In actuality, the “Strong Nuclear Force” (Nuclear Gravitation Field) at the surface of the nucleus becomes much weaker, therefore, the Space-Time Compression associated with the Nuclear Gravitation Field is reduced as the nucleus is stretched.  The measured “Strong Nuclear Force” outside the atom becomes much more intense in like manner to the isotope ₈₃Bi²⁰⁹ (Bismuth) because of the more gradual “drop off” of the intensity of the “Strong Nuclear Force” within the atom.

Index and Direct Links to Other Chapters of Nuclear Gravitation Field Theory
and Nuclear Gravitation Field Theory Home Page/Table of Contents:

Nuclear Gravitation Field Theory

1. Purpose for Evaluation of the Strong Nuclear Force and the Force of Gravity



2. Executive Summary



3. The Classical Physics Evaluation of Electrostatics and Gravity
1. The Electrostatic Repulsion Force
2. Newton’s Law of Gravity - The Attractive Force of Masses
3. Comparison of Electrostatic Repulsion and Gravitational Attraction



4. Nuclear Gravitation Field Theory:  Major Stumbling Blocks to Overcome



5. New Theory Results Must Equal Old Theory Results When and Where Applicable
1. Newton’s Law of Gravity as It Applies to Large Masses and Nuclear Gravitation Field Theory
2. Kepler’s Laws, Gravity, and Nuclear Gravitation Field Theory



6. Structure of the Nucleus of the Atom



7. The Schrodinger Wave Equation and Quantum Mechanics - The Particle and Wave Characteristics of Matter



8. Nuclear Gravitation Field Theory Versus Accepted Strong Nuclear Force Overcoming Electrostatic Repulsion



9. Comparison of the Nuclear Gravitation Field to the Gravitational Field of the Sun and the Gravitational Field of a Neutron Star



10. Quantum Mechanics, General Relativity, and the Nuclear Gravitation Field Theory



11. Properties of the Strong Nuclear Force, Nuclear Properties of Bismuth, and the Nuclear Gravitation Field Theory



12. Conclusion



13. Appendix A:  References



14. Appendix B:  Background of the Author

Index and Direct Hyperlinks to the Other Web Pages on this Website:

1. Gravity Warp Drive Home Page



2. Nuclear Gravitation Field Theory  (Specific Chapter Links are Provided on this Web Page)



3. Purchase e-Books



4. History of My Research and Development of the Nuclear Gravitation Field Theory



5. “The Zeta Reticuli Incident” by Terence Dickinson



6. Supporting Information for the Nuclear Gravitation Field Theory



7. Government Scientist Goes Public



8. “Sport Model” Flying Disc Operational Specifications



9. Design and Operation of the “Sport Model” Flying Disc Anti-Matter Reactor



10. Element 115



11. Bob Lazar’s Gravity Generator



12. United States Patent Number 3,626,605:  “Method and Apparatus for Generating a Secondary Gravitational Force Field”



13. United States Patent Number 3,626,606:  “Method and Apparatus for Generating a Dynamic Force Field”



14. V. V. Roschin and S. M. Godin:  “Verification of the Searl Effect”



15. The Physics of Star Trek and Subspace Communication:  Science Fiction or Science Fact?



16. Constellation:  Reticulum



17. Reticulan Extraterrestrial Biological Entity



18. Zeta 2 Reticuli:  Home System of the Greys?



19. UFO Encounter and Time Backs Up



20. UFO Testimonies by Astronauts and Cosmonauts and UFO Comments by Presidents and Top U.S. Government Officials



21. Pushing the Limits of the Periodic Table



22. General Relativity



23. Rethinking Relativity



24. The Speed of Gravity - What the Experiments Say



25. Negative Gravity



26. The Bermuda Triangle:  Space-Time Warps



27. The Wright Brothers



28. Website Endorsements and Favorite Quotes



29. Sponsors of This Website



30. Romans Road to Eternal Life In Jesus Christ

© Copyright Kenneth F. Wright, April 10, 2000.
All rights reserved.  No portion of this document may be
reproduced in any form without written permission of the author.