
This is the English translation of a Web Page originally written in French, by Nymbus, who also provided the translation. I have posted it here at my own Website, with some minor personal additional comments. The content has been left untouched. Any comments or questions should be addressed to nymbus@wanadoo.fr. At times, this Web Page alludes to concepts from Einstein’s Special Relativity Theory.
Minor editing, the Space-Time Compression description, and the Conclusions were provided by Ken Wright.
Reference: http://www.svsu.edu/~slaven/gr/
NOTE: The above reference link appears to be no longer active.
![]()
![]()
Before beginning this brief article, dealing with the essential features of General Relativity, we have to postulate one thing: Special Relativity is supposed to be true. Hence, General Relativity lies on Special Relativity. If the latter were proved to be false, the whole edifice would collapse.
In order to understand General Relativity, we have to define how mass is defined in classical mechanics.
The Two Different Manifestations of Mass:
First, let’s consider what represents mass in everyday life: “It’s weight.” In fact, we think of mass as something we can weigh, as that’s how we measure it: We put the object whose mass is to be measured on a balance. What’s the property of mass we use by doing this? The fact that the object and Earth attract each other. To be convinced of it, just go in your garage and try to raise your car! This kind of mass is called “gravitational mass.” We call it “gravitational” because it determines the motion of every planet or of every star in the universe: Earth’s and Sun’s gravitational mass compels Earth to have a nearly circular motion around the latter.
Now, try to push your car on a plane surface. You cannot deny that your car resists very strongly to the acceleration you try to give it. It is because the car has a very large mass. It is easier to move a light object than a heavy one. Mass can also be defined in another way: “It resists acceleration.” This kind of mass is called “inertial mass.”
We thus arrive at this conclusion: We can measure mass in two different ways. Either we weigh it (very easy...) or we measure its resistance to acceleration (using Newton’s law).
Many experiments have been done to measure the inertial and gravitational mass of the same object. All lead to the same conclusion: The inertial mass equals the gravitational mass.
Newton himself realized that the equality of the two masses was something his theory couldn’t explain. But he considered this result as a simple coincidence. On the contrary, Einstein found that there lay in this equality a way to supplant Newton’s theory.
Everyday experimentation verifies this equality: Two objects (one heavy and the other one light) “fall” at the same speed. Yet, the heavy object is more attracted by Earth than the light one. So, why doesn’t it fall “faster?” Because its resistance to acceleration is stronger. From this, we conclude that the acceleration of an object in a gravitational field doesn’t depend upon its mass. Galileo Galilei was the first one to notice this fact. It is important that you should understand that the fact that all objects “fall at the same speed” in a gravitational field is a direct consequence of the equality of inertial and gravitational masses (in classical mechanics).
Now, I would like to focus on the expression “to fall.” The object “falls” because of Earth’s gravitational field generated by Earth’s gravitational mass. The motion of the two objects would be the same in every gravitational field, be it Moon’s or Sun’s. They accelerate at the same rate. It means that their speeds increase by the same value in every second (Acceleration is the value by which speeds increases in one second).
The Equality of Gravitational and Inertial Masses as an Argument for Einstein’s Third Postulate:
Einstein was looking for something which could explain this: “Gravitational mass equals inertial mass.”
Aiming at this, he stated his third postulate, known as the principle of equivalence. It says that if a frame is uniformly accelerated relative to a Galilean one, then we can consider it to be at rest by introducing the presence of uniform gravitational field relative to it.
Let’s consider a frame K', which has a uniformly accelerated motion relative to K, a Galilean frame. There are many objects around K and K'. These objects are at rest, relative to K. So, these objects, relative to K', have a uniformly accelerated motion. This acceleration is the same for all objects, and it is opposed to the acceleration of K' relative to K. We have just said that all objects accelerate at the same rate in a gravitational field. So, the effect is the same as if K' is at rest and that a uniform gravitational field is present.
Thus, if we state the principle of equivalence, the equality of the two masses is a simple consequence of it. That’s why this equality is a powerful argument in favor of the principle of equivalence.
By supposing K' is at rest and a gravitational field is present, we make of K' a Galilean frame, where we can study the laws of mechanics. That’s why Einstein stated his fourth principle:
Einstein’s Fourth Postulate:
Einstein’s fourth postulate is a generalization of the first one. It can be expressed in the following way: “The laws of nature are the same in every frame.” It cannot be denied that it is more “natural” to say that the laws of nature are the same in every frame than in Galilean ones. Moreover, we don’t really know if a Galilean frame really exists.
This principle is called the “Principle of General Relativity.”
| The Deadly Lift: Let’s consider a lift in free fall, falling within a very high skyscraper with a foolish man inside it. Refer to Figures 1, 2, and 3 to the right. In Figure 1, the man lets his watch and his handkerchief fall. What happens? For someone watching the fall from outside the lift, whose frame is Earth’s, the watch, the handkerchief, the man and the lift fall at exactly the same speed (Let’s remember that the motion of a body in a gravitational field doesn’t depend upon its mass, according to the equivalence principle). Thus, the distance between the watch and the floor, or between the handkerchief and the floor, or between the man and the watch, or between the man and the floor... doesn’t vary. Therefore, for the man inside the lift, the watch and the handkerchief will stay where he left them. Now, if the man gives his watch or his handkerchief a certain speed, they will follow a straight line at a constant speed. This leads to the following conclusion: The man inside the lift can ignore Earth’s gravitational field. The lift behaves like a Galilean frame. However, it will not last forever. Sooner or later, the lift will crash, and the observer outside the lift will attend to a great slaughter! |
 Figure 1: |
| Now, let’s do a second idealized experiment: In Figure 2, our lift is far away from any great mass, in deep space for example. Our foolish man has survived his accident, and, after several years in a hospital (years, with respect to what?...), he decides to go back in the lift. Suddenly, a being (what kind of being, we don’t know, ask Mulder for the answer) begins to pull the lift: Classical mechanics tells us something: a constant force provokes a constant acceleration (This is not true at very high speeds, as the mass of an object increases with its velocity; however, we will consider it as true for our experiment). Hence, the lift will have an accelerated motion in any Galilean frame. Our guinea pig inside the lift lets his handkerchief and his watch fall. Someone outside the lift in a Galilean frame thinks that the watch and the handkerchief will hit the floor, as the latter will catch up with them because of its acceleration. In fact, the observer outside the lift will see the distance between the watch and the floor and the distance between the handkerchief and the floor diminish at the same rate. On the other hand, the man inside the lift will notice that his watch and his handkerchief have the same acceleration. He will attribute it to a gravitational field. These two interpretations seem equally true: On the one side, an accelerated motion, on the other side, a uniform motion and the presence of a gravitational field. |
 Figure 2: |
| Let’s do another test to justify the presence of a gravitational field. In Figure 3, a ray of light gets into the lift through a window and hits the wall facing it. Here are the two interpretations of our observers: The one outside the lift tells us: “Light gets into the lift though the window horizontally in a straight line and at a constant speed (of course!) toward the opposite wall. But the lift is going upward: thus, the light will hit the wall not exactly in front of its entry point, but a little bit lower.” The man inside the lift says: “I am in presence of a gravitational field. As light has no mass, it will be spared the field’s effects, and it will hit the wall exactly in front of its point.” Oops! A problem! The two observers don’t agree. However, the man inside the lift has made a mistake. He said that light has no mass. But light carries energy, which has a mass (remember that E = Mc2, therefore, the mass of a Joule of Energy is: m = E/c2...). Hence, light will have a curved trajectory towards the floor, as the observer outside the lift said. |
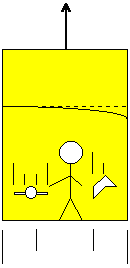 Figure 3: |
As the mass of energy is very small (c2 = {299,750,000 meters/sec}2!), the phenomenon can only be detected in the presence of VERY strong gravitational fields. It has been verified thanks to the Sun’s great mass: rays of light are curved when they approach it. This experiment was the first confirmation of Einstein’s theory.
All these experiments allow us to conclude: We can consider that an accelerated frame is a Galilean one by introducing the presence of a gravitational field. Furthermore, it is true for all kinds of motions, be they rotations (the gravitational field explains the presence of centrifugal forces) or not uniformly accelerated motions (which is translated mathematically by the fact that the field doesn’t satisfy Riemann’s condition). As you see, the principle of General Relativity is fully in accordance with experience!

Figure 4:
The Equivalence of Acceleration and a Gravity Field
Elevators in Acceleration
NB: This example is drawn from “L’évolution des idées en Physique” (Champs Flammarion 1982) written by Albert Einstein and Leopold Infeld. A marvelous book! Read it if you have any interest in physics in general. Fascinating!
Universe’s Geometry:
Now, things are going to be very very weird. I’m sure you were astonished when you discovered time dilation. But Einstein also discovered another strange consequence of his postulates: The world in which we live is not Euclidean (in most cases). This means that circles are not round, that parallel lines can cross or diverge and that the angles of a triangle may not add up to 180°!
But be careful! I don’t say that what you learned at school is false! Euclidean geometry, as a mathematical abstraction, is always true. But when it comes to describing the real world, nothing is sure. Before Einstein discovered that Euclidean geometry was not the one which described the world, Gauss and later Riemann developed another kind of geometry. It is sometimes called “Gaussian geometry.” When they developed this new branch of math, they couldn’t even imagine that it was to be the proper description of the world. In fact, Einstein, helped by his friend Grossman (a good mathematician) developed his General Theory of Relativity on the basis of Gaussian geometry. What I want to show is that math is developed without any reference to the world. It’s an “abstraction.”
Let’s take another example: 1 + 1 = 2. Is it true? As a mathematical abstraction, always true. But when you want to give this expression a physical meaning, it is sometimes false. For instance, you cannot add the speed of light to another speed (remember the experience with the train, we couldn’t add the speed of photons to the speed of the train): “v + c = c.” If you add one liter of milk to one liter of water, you will not obtain 2 liters of liquid. Do you see what I mean? Math is certain as long as they don’t refer to reality. It is very important that you should understand this. Now, let’s go back to General Relativity.
Let’s consider a huge disk above which are drawn two concentric circles, one very small and the other one as huge as the disk as displayed in Figure 5, below:
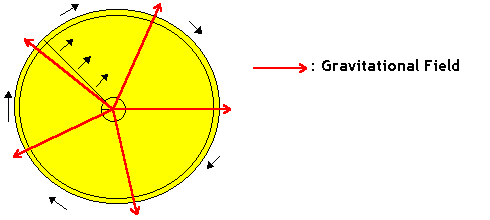
Figure 5: Rotating Discs in a Gravity Field
Our observer is on the disk, which rotates at a very high speed. Another man, in a Galilean frame, measures the circumferences (P) of the two circles, and their diameters (d) with a ruler. This man then does the following calculus: P/d. He finds: P/d = π. For him, Euclidean geometry is true (true means here that it describes reality).
The observer on the disk measures the circumferences and the diameters WITH THE SAME RULER. For the measurement of the diameters, the ruler is not contracted (from the point of view of the man in the Galilean frame) in its length (see Special Relativity for this). Thus, the observer on the disks will find the same results as the man in the Galilean frame.
Now, the observer measures the circumference of the small circle. For the man outside the disk, the rule is not contracted in its length because it goes very slowly (it’s close to the center of the disk). Therefore, the observer finds again the same result.
However, things are going to be different for the fourth measurement. When the observer on the disk measures the circumference of the big circle, he goes very fast compared to the man outside the disk. Hence, from the point of view of this man, the rule is contracted in its length and the observer won’t find the same result. For him: P/d does not equal π. Euclidean geometry doesn’t describe reality in this case.
What can account for this strange result? The observer on the disk, when measuring the circumference of the big circle, experienced a strange force. You would call it a “centrifugal force.” It’s due to the presence of a gravitational field (symbolized on the diagram by arrows).
The same experiment could be done to measure time by using a clock in the three different frames: In the Galilean frame, on the disk close to its center and far from it. It would lead us to the same conclusion: When the observer on the disk is far from its center, his measurement of time is different from the man’s outside the disk. The presence of a gravitational field could account for the difference.This leads us to the following conclusion: a gravitational field influences time and space.
Time dilation due the presence of a gravitational field has been measured. In fact, the value of this field at the top of a high mountain is slightly less than its value at the bottom of the mountain as indicated by Figure 6, below. Two atomic clocks initially synchronized gave two different results after having spent a while in these two different places:
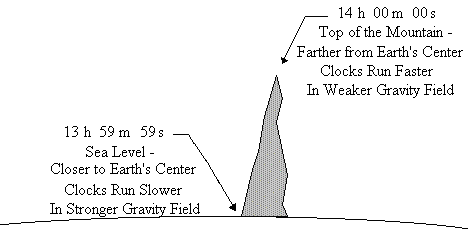
Figure 6: Gravity Field and Clock Speed
Space-Time Compression:
What is Space-Time Compression and how is it related to Special Relativity and General Relativity? Space-Time Compression is the relativistic effect of reducing the measured distance and light travel-time between two points in space as a result of the presence of either:
- Two or more inertial reference frames where relativistic velocities (velocities of a significant fraction of the velocity of light) between the reference frames are involved -- an example of Special Relativity. A specific example of applied Special Relativity with two inertial reference frames is a spacecraft traveling at 0.98c (98% of the velocity of light) as measured by an observer on Earth and the observer’s position on Earth.
- Accelerated reference frames defined by either the physical acceleration, or change in velocity, of an object of interest relative to a point of reference in Space-Time in the presence of an acceleration field -- General Relativity. An example of an accelerated reference frame is that of the Sun’s gravitational field, equal to 27.8g, near the Solar surface.
Space-Time Compression occurs because of the invariance of the measured, or observed, velocity of light independent what inertial or accelerated reference frame the observer exists within or externally observes.
Inertial Reference Frames:
One way to quantitatively observe the Space-Time compression effect is to look at the blue right triangle within a quarter circle of unity radius (radius, r = 1) displayed in Figure 7, below. The hypotenuse of the triange is the side of the blue triangle starting from the center of the circle moving diagonally upward and to the right with a length unity, or 1, and equal to the radius of the quarter circle. The hypotenuse of the blue right triangle represents the velocity of light, c, as a fraction of the velocity of light, c, which, of course, is c/c = 1. The vertical side of the blue right triangle is the ratio of the velocity of the spacecraft to that of the velocity of light, or v/c. The vertical side of the blue right triangle is the “opposite side” from the angle formed by the hypotenuse of the blue right triangle, or the radius of the quarter circle, and the horizontal side of the blue right triangle. That angle is represented by the Greek letter θ (Theta). The angle θ spans from 0° to 90°. The length of the vertical side of the blue right triangle is equal to sinθ, therefore, v/c = sinθ. The horizontal side of the blue right triangle represents the amount of Space-Time Compression that reduces the distance between two points in Space-Time (length contraction) and reduces the time it takes light to travel between the two points (time dilation) based on the velocity of the spacecraft relative to the velocity of light. The length of the horizontal side of the blue right triangle is equal to cosθ. The “Space-Time Compression Factor” is the multiplicative inverse of the value of length of the horizontal side of the blue right triangle equal to 1/cosθ, or secθ, and is designated by the Greek Letter γ (Gamma). The length contraction and time dilation can be determined by solving for the length of the horizontal side of the triangle using the Pythagorean Theorem.
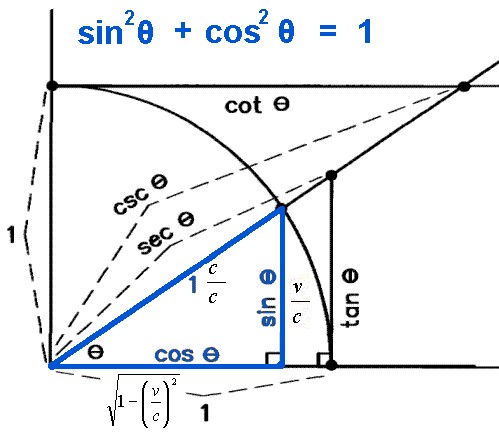
Figure 7: Application of Pythagorean Theorem
to Special Relativity
sin2θ + cos2θ = 1
v/c = sinθ
Substitute v/c for sin θ, then solve for cosθ
(v/c)2 + cos2θ = 1
cos2θ = 1 – (v/c)2
cosθ = [1 – (v/c)2]1/2
1/cosθ = secθ = 1/[1 – (v/c)2]1/2 = “Space-Time Compression Factor”
Therefore, the distance between the Earth and the star of interest 10 light-years away as measured by the observer in the spacecraft moving at a velocity, v, is defined as follows:
d = d0 [1 – (v/c)2]1/2
Where d0 is the measured distance to the star of interest in “Normal Space-Time” or “Uncompressed Space-Time” as measured by the observer on the Earth and d is the “Compressed Space-Time” distance (or length contracted distance) as measured by the observer in the spacecraft moving at a velocity, v. The reduction of time for light to travel the distance between the star of interest and spacecraft in the vicinity of Earth is affected in the same manner by “Space-Time Compression.” Einstein noted the equivalence of space and time, hence the term Space-Time is used. The relationship of space and time is as follows:
d = ct
d represents distance, c represents the velocity of light, and t represents elapsed time. Substituting ct for d and ct0 for d0, the distance compression equation can become a time dilation equation.
ct = ct0 [1 – (v/c)2]1/2
Therefore: t = t0 [1 – (v/c)2]1/2
The following table provides the values for length contraction and “Space-Time Compression Factor” as a function of velocity relative to the velocity of light, c = 299,755 km/sec = 186,300 miles/sec.
Angle θ Degrees |
Measured Velocity = v = (c)(sinθ) v/c = sinθ |
Distance (Length) Contraction or Time Dilation Factor = cosθ = [1 – (v/c)2]1/2 |
Space-Time Compression Factor = γ = 1/cosθ = secθ = 1/[1 – (v/c)2]1/2 |
Effective Velocity = veff = (c)(tanθ) = (c)(sinθ/cosθ) [veff/c] = tanθ |
|---|---|---|---|---|
| 0.000 | 0.000 | 1.000 | 1.000 | 0.000 |
| 2.866 | 0.050 | 0.999 | 1.001 | 0.050 |
| 5.739 | 0.100 | 0.995 | 1.005 | 0.101 |
| 8.627 | 0.150 | 0.989 | 1.011 | 0.152 |
| 11.537 | 0.200 | 0.980 | 1.021 | 0.204 |
| 14.478 | 0.250 | 0.968 | 1.033 | 0.258 |
| 17.458 | 0.300 | 0.954 | 1.048 | 0.314 |
| 20.487 | 0.350 | 0.937 | 1.068 | 0.374 |
| 23.578 | 0.400 | 0.917 | 1.091 | 0.436 |
| 26.744 | 0.450 | 0.893 | 1.120 | 0.504 |
| 30.000 | 0.500 | 0.866 | 1.155 | 0.577 |
| 33.367 | 0.550 | 0.835 | 1.197 | 0.659 |
| 36.870 | 0.600 | 0.800 | 1.250 | 0.750 |
| 40.542 | 0.650 | 0.760 | 1.316 | 0.855 |
| 44.427 | 0.700 | 0.714 | 1.400 | 0.980 |
| 45.000 | 0.707 | 0.707 | 1.414 | 1.000 |
| 48.590 | 0.750 | 0.661 | 1.512 | 1.134 |
| 53.130 | 0.800 | 0.600 | 1.667 | 1.333 |
| 58.212 | 0.850 | 0.527 | 1.898 | 1.614 |
| 60.000 | 0.866 | 0.500 | 2.000 | 1.732 |
| 64.158 | 0.900 | 0.436 | 2.294 | 2.065 |
| 71.805 | 0.950 | 0.312 | 3.203 | 3.042 |
| 73.739 | 0.960 | 0.280 | 3.571 | 3.428 |
| 75.930 | 0.970 | 0.243 | 4.113 | 3.990 |
| 78.522 | 0.980 | 0.199 | 5.025 | 4.925 |
| 81.890 | 0.990 | 0.141 | 7.470 | 7.018 |
| 84.268 | 0.995 | 0.100 | 10.013 | 9.962 |
| 85.000 | 0.996 | 0.087 | 11.474 | 11.430 |
| 85.561 | 0.997 | 0.077 | 12.920 | 12.882 |
| 86.376 | 0.998 | 0.063 | 15.819 | 15.789 |
| 87.437 | 0.999 | 0.045 | 22.366 | 22.340 |
As indicated in Table 1, above, measured velocities do not contribute significantly to the “Space-Time Compression” effect unless the measured velocity is a significant fraction of the velocity of light, c. At a measured velocity of 0.995c, the “Space-Time Compression Factor” is just above 10 and at a measured velocity of 0.999c, the “Space-Time Compression Factor” is just under 22.4.
Table 1 introduces the concept of effective velocity. When the spacecraft is traveling at a measured velocity of 0.707c, the effective velocity, veff, of the spacecraft is 1.000c or the speed of light, c. Although the spacecraft only has a measured velocity as 0.707c, the length contraction along the line of travel is reduced to 0.707 (or 70.7%) of the original distance (which represents a “Space-Time Compression Factor” equal to 1.414), therefore, the time to travel the uncompressed distance (which is a known quantity) is equal to the time it would take light to travel the uncompressed distance.
EXAMPLE:
Let’s assume our astronaut is traveling from the Earth to a star system 10 light-years distant. The astronaut is traveling at a measured velocity of 0.707c. The astronaut measures the distance to the star system as only 7.07 light-years rather than 10 light-years because of the relativistic length contraction in the direction of motion. The astronaut’s travel time to the star system is 10 years as measured by the astronaut. The observer on Earth watching the astronaut accomplish the trip disagrees on the time elapsed. The observer on earth agrees with the astronaut that the astronaut’s measured velocity is 0.707c. However, the observer on Earth measures the distance the astronaut must travel as 10 light-years (the Uncompressed Space-Time distance). The observer on Earth measures the time elapsed for the astronaut to accomplish the trip from Earth to the star system as 14.1 years. Realize that it takes time for the light to travel from our astronaut’s position back to earth resulting in the disagreement on the time required for the astronaut to make the trip.
If a person could, theoretically, accelerate to the actual measured velocity of light, c, then the distance required to be traveled would be compressed to zero length. In this case, the effective velocity, veff would be infinity and zero time would be required to travel the distance because the distance is now zero. With measured velocities very close to that of the speed of light, c, the effective velocity, veff approaches the Space-Time Compression Factor. Therefore, because of the “Space-Time Compression” phenomenon, one could effectively travel much faster than the speed of light. The relationship between measured velocity, v, effective velocity, veff, and “Space-Time Compression Factor” is defined by the relationship of the various trigonometric functions.
If angle θ is very small (i.e., angle θ ≈ 0°),
then tanθ ≈ sinθ
because cosθ ≈ 1.000
Likewise, if v << c
(i.e., measured velocity is insignificant relative to the speed of light),
then veff ≈ v
If angle θ → 90° (i.e., angle θ is approaching 90°)
then tanθ ≈ 1/cosθ = secθ → ∞
because sinθ ≈ 1.000
Likewise, if v → c
(i.e., measured velocity is approaching the speed of light)
then effective velocity, veff ≈ Space-Time Compression Factor → ∞
Analysis of Two Hypothetical Inertial Reference Frames:
Let’s look at Space-Time Compression in two hypothetical relativistic inertial reference frames. Consider an observer on Earth looking at a star 10 light-years distant and an observer on a spacecraft traveling at a velocity, v = 0.98c, which is a significant fraction of the velocity of light, c. The light propagating from the star is measured to be moving at a velocity of c by both the observer on Earth and the observer in the spacecraft traveling at 0.98c. Recall that the velocity of light will always be measured the same in a vacuum, no matter what inertial reference frame the observer is in. We cannot add the velocity of our spacecraft to the velocity of light and get a result for the velocity of light other than c because the speed of photon propagation in a vacuum will always be measured as c no matter what reference frame one exists in when measuring the speed of light. Therefore, “v + c = c.” This “strange math” works out because we are adding velocities. A velocity is defined as a change in position of an object or particle with respect to some measured elapsed time. The “strange math” occurs because the measured elapsed time is different for observers in different inertial reference frames. We will compare what each observer sees at the instant the observer in the spacecraft passes by the Earth and the observer on the Earth. The observer in the spacecraft and the observer on Earth disagree on the distance to the star and the amount of time it takes light to travel from the star to each of them. The observer on Earth measures the distance as 10 light-years. The observer in the spacecraft, however, measures the distance to the star to be about 2 light-years because the Space-Time Compression factor for traveling at 0.98c is equal to 5.025 resulting in his/her observed length contraction. In addition, because of the shorter measured distance, the time it takes the light to travel from the star to the observer on the spacecraft is only about 2 years because of the length contraction. To the observer on Earth, it appears to take the spacecraft over 10 years to arrive at the star. The disagreement between the observer in the spacecraft and the Earth observer for the time it takes the spacecraft to travel the distance to the star occurs because of the delay time for the light from the spacecraft to return back to Earth. If the spacecraft is 10 light-years away, it will take 10 years for the light from the spacecraft to reach Earth. This hypothetical scenario demonstrates the equivalence of space (distance) and time.
One other concept that is observed here is that of “effective velocity.” The “effective velocity” represents the velocity of the spacecraft relative to Normal Space-Time rather than Compressed Space-Time. This would be the case if the velocity of light was infinite. The observer in the spacecraft realizes that the normal space-time distance to the star is 10 light-years even though, with the spacecraft measured velocity of 0.98c relative to Earth, the Compressed Space-Time distance measured to the star is 2 light-years. Therefore, the effective velocity of the spacecraft is about 5 times the speed of light because it takes the observer 2 years, as measured by spacecraft onboard clock, to travel the Normal Space-Time distance of 10 light-years to the star. If the spacecraft was traveling at 0.7071c to the star 10 light-years away, the measured Compressed Space-Time distance to the star would be 7.071 light-years. The time it would take the spacecraft to travel the Compressed Space-Time distance of 7.071 light-years would be 10 years, as measured by the spacecraft onboard clock. Therefore, the effective velocity of the spacecraft is equal to the speed of light. The observer on Earth, however, would measure the time elapsed for the spacecraft to travel the actual 10 light-year distance to the star as 14.142 years. That time is consistent with the measured velocity of the spacecraft relative to the Earth observer of 0.7071c. The additional 4.142 years that elapses for the spacecraft trip, as measured by the observer on Earth, results from the fact that it takes time for the light to return to Earth from the spacecraft, as the spacecraft travels to the star. From the right triangle and Pythagorean Theorem, one can see that sin θ represents the measured velocity of the spacecraft and tan θ represents the effective velocity of the spacecraft. If the spacecraft could have an actual velocity of the speed of light (sin θ = 1), then the effective velocity would be infinity (tan θ = infinity). Space-time would be compressed to zero length based upon traveling at the speed of light.
Let’s look at the Flying Disc Spacecraft traveling at 0.98c relative to Earth as it passes over an Aircraft Hanger on the Earth from left to right. We will examine what an observer in front of the Aircraft Hanger on Earth at rest relative to the Aircraft Hanger would see as the Flying Disc Spacecraft passes above the Aircraft Hanger. We will compare that observation to what an observer in a second spacecraft flying in the same direction as the Flying Disc Spacecraft at a velocity of 0.98c such that the Flying Disc Spacecraft appears to be at rest relative to this second observer. Figure 8, below, displays the Flying Disc Spacecraft hovering over the Aircraft Hanger such that the Flying Disc Spacecraft is “at rest” relative to the Aircraft Hanger. The Flying Disc Spacecraft is 300 feet in diameter and the Aircraft Hanger is 300 feet in width from left to right. Therefore, when both the Flying Disc Spacecraft and the Aircraft Hanger are at rest relative to each other, they appear to be the same width.

Figure 8:
Aircraft Hanger 300 Feet Wide and
Flying Disc Spacecraft 300 Feet in Diameter
Both At Rest In Same Reference Frame
First we will analyze what the observer on Earth in front of the Aircraft Hanger sees as the Flying Disc Spacecraft passes over the Aircraft Hanger. As the Flying Disc Spacecraft passes over the Aircraft Hanger, we will focus on four specific events noted by the observer on Earth. Refer to Figure 9, below:

Figure 9:
Flying Disc Spacecraft Moving from Left to Right
at 98% Velocity of Light Over Aircraft Hanger
Observer At Rest Relative to Aircraft Hanger
Note in Figure 9, above, that the Flying Disc Spacecraft is “compressed” by a factor of 5 in width along its direction of motion. This represents the “Space-Time Compression” in the direction of motion of the Flying Disc Spacecraft as seen by the observer on Earth because its velocity relative to the observer on Earth is 0.98c (See Table 1, above). The events of interest as seen by the observer on Earth in front of the Aircraft Hanger as the Flying Disc Spacecraft passes over the Aircraft Hanger from left to right are as follows in order of the occurrence of each of those events.
| Event 1: | The leading edge of the Flying Disc Spacecraft aligns with the left side of the Aircraft Hanger. |
| Event 2: | The lagging edge of the Flying Disc Spacecraft aligns with the left side of the Aircraft Hanger. |
| Event 3: | The leading edge of the Flying Disc Spacecraft aligns with the right side of the Aircraft Hanger. |
| Event 4: | The lagging edge of the Flying Disc Spacecraft aligns with the right side of the Aircraft Hanger. |
Now we will analyze what the observer on the second spacecraft flying with the Flying Disc Spacecraft at 0.98c relative to Earth and the Aircraft Hanger sees as the Flying Disc Spacecraft passes over the Aircraft Hanger. Just as with the observer at rest on Earth in front of the Aircraft Hanger, above, we will focus on four specific events as the Flying Disc Spacecraft passes over the Aircraft Hanger. However, the events will be noted as seen by the observer in the second spacecraft. Refer to Figure 10, below:

Figure 10:
Flying Disc Spacecraft Moving from Left to Right
at 98% Velocity of Light Over Aircraft Hanger
Observer At Rest Relative to Flying Disc Spacecraft
Now note in Figure 10, above, that the Aircraft Hanger, rather than the Flying Disc Spacecraft, has a “compressed” width along the direction of motion of the Flying Disc Spacecraft. The Flying Disc Spacecraft appears to have full width. This represents the “Space-Time Compression” in the direction of motion of the Flying Disc Spacecraft as seen by the second observer in the observing from the second spacecraft. Because the second spacecraft is flying with the Flying Disc Spacecraft, the Flying Disc Spacecraft appears to be at rest relative to the second spacecraft, hence, appears to be of full width in the direction of motion. The Earth and the Aircraft Hanger appear to be moving at a velocity of 0.98c from right to left relative to both the spacecraft in motion resulting in the Aircraft Hanger appearing to be “compressed” in width by a factor of 5 along the direction of motion of the Flying Disc Spacecraft (see Table 1, above). The events of interest as seen by the observer in the second spacecraft as the Flying Disc Spacecraft passes over the Aircraft Hanger from left to right are as follows in order of the occurrence of each of those events.
| Event 1: | The leading edge of the Flying Disc Spacecraft aligns with the left side of the Aircraft Hanger. |
| Event 2: | The leading edge of the Flying Disc Spacecraft aligns with the right side of the Aircraft Hanger. |
| Event 3: | The lagging edge of the Flying Disc Spacecraft aligns with the left side of the Aircraft Hanger. |
| Event 4: | The lagging edge of the Flying Disc Spacecraft aligns with the right side of the Aircraft Hanger. |
There is an obvious disparity between the observations of the two observers. The first observer is on Earth at rest relative to the aircraft hanger and the second observer is onboard a second spacecraft moving at a velocity of 0.98c in parallel with the Flying Disc Spacecraft, therefore, at rest relative to the Flying Disc Spacecraft. The two observers disagree with the order of the events taking place as the Flying Disc Spacecraft flies over the aircraft hanger. The event the Earth observer identifies as “Event 2” is identified as “Event 3” by the observer on the second spacecraft. Likewise, the event the Earth observer identifies as “Event 3” is identified as “Event 2” by the observer on the second spacecraft. Although the time interval between “Event 2” and “Event 3” is on the order of only 300 nanoseconds (300 x 10–9 seconds), there is a reversal of the order of the events in Space-Time. This hypothetical situation demonstrates that the times of occurrence of events are relative to the specific reference frames of the observers and are not absolutes. Observers in different reference frames will not agree on the order of events, nor will they agree on the simultaneity of events. This disagreement in the order of events in time provides the evidence that time-travel is, theoretically, possible. If the Space-Time Compression factor is large enough, then events that are years apart could be reversed relative to observers in different reference frames. Large Space-Time Compression factors could, theoretically, be generated by amplifying gravity in a local area to generate separate accelerated reference frames (see the following discussion on accelerated reference frames). The “The Philadelphia Experiment and the Secrets of Montauk” Website provides testimony from several individuals regarding their involvement with the U.S. Government’s Top Secret time-travel experiments. It has been speculated that Albert Einstein and John Von Neumann were both involved with the Philadelphia Experiment. It has been speculated that John Von Neumann was intimately involved with the Phoenix Project, also known as the Montauk Project.
Gravity Accelerated Reference Frames:.
| When “Relativity is Generalized” to include the effects of gravity and accelerated reference frames, the equations of relativity predict that gravity, or the curvature of Space-Time by matter, not only stretches or shrinks distances (depending on their direction with respect to the gravitational field) but also will appear to slow down or “dilate” the flow of time -- the very definition of Space-Time Compression. The equations used to represent the curvature of Space-Time in gravitational fields are multi-dimensional, rather complicated, and dependent upon the geometry of the system of interest. In most circumstances throughout the universe the intensity of the local gravitational field at a point in Space-Time is relatively small, hence, any Space-Time Compression taking place in that locality is miniscule. However Space-Time Compression can become significant at a locality when Space-Time is curved by a strong gravitational field produced by a massive object such as a star like our Sun as indicated by Figure 11 and Figure 12. |  Figure 11: |

Figure 12: Sun’s Gravity Distorting Space-Time
| Just as the velocity of light in a vacuum will always be measured as c no matter what velocity of travel of the observer, the velocity of light will always be measured as c in an accelerated reference frame, no matter how great the acceleration or gravitational field. Einstein’s General Relativity Theory states that light is accelerated by a gravitational field, which results in the observed “bending of light” around our Sun as indicated by Figure 11, above. This appears to be a paradox. How can light be accelerated, yet remain at a velocity of c? Lets take a look at a rubber ball that is dropped in Earth’s gravitational field as displayed in Figure 13. The ball is initially at rest. When released, the ball begins to fall and its velocity of fall rises as it is accelerated by the local gravitational field of Earth until the rubber ball finally hits the floor. Graphs of the ball fall distance and ball velocity as a function of time are provided in Figure 14 and Figure 15, respectively, below. The graphs assume continual free-fall. A photon of light is accelerated by a gravitational field in like manner to our ball falling in Earth’s gravitational field. However, instead of the photon of light traveling faster and faster relative to an external observer as our falling ball does, the distance the photon of light travels (and the time it takes the photon of light to travel that distance) compresses in a manner to offset the acceleration by gravity so that the velocity of the photon of light always remains the same, equal to c, relative to the external observer. This Space-Time Compression effect is miniscule in Earth’s gravitational field because the gravitational field is relatively weak and the Earth’s average diameter, 7,918 miles, is relatively small compared to the distance light can travel in one second, 186,300 miles or 299,750 kilometers. A photon of light energy will travel a distance of about 7.5 Earth circumferences in one second (Earth’s circumference is about 25,000 miles). When at or above the Earth’s surface, the Earth’s gravitational field intensity drops off proportional to 1/r2 where r represents the distance from the Earth’s center (Newton’s Law of Gravity). Earth’s gravitational field is equal to 1g = 32.2 feet/second2 acceleration = 0.00610 miles/second2 acceleration at the Earth’s surface, which is just under 4,000 miles from the Earth’s center. At about 4,000 miles above the Earth’s surface, the gravitational field is only 0.25g = 8.05 feet/second2 acceleration = 0.00152 miles/second2 acceleration. The change in velocity -- actually the amount of Space-Time Compression (photon of light velocity will always be measured at 186,300 miles/second) -- resulting from a photon of light traveling at 186,300 miles/second spending 1 second in Earth’s gravitational field is very miniscule. A photon of light spends very little time in the Earth’s gravitational field, therefore, is not significantly affected by the Earth’s gravitational field. What we conclude here is the amount of Space-Time Compression that occurs due to a gravitational field is a function of both the intensity of the gravitational field and the amount of time that a photon of light remains within the gravitational field. Gravitational fields are acceleration fields. The final velocity of an object in an acceleration field is a function of the rate of acceleration in that field and the time that acceleration is applied to an object in the field. An acceleration is a rate of change of velocity as a function of time. |
 Figure 13: |
|
 Figure 14: |
||
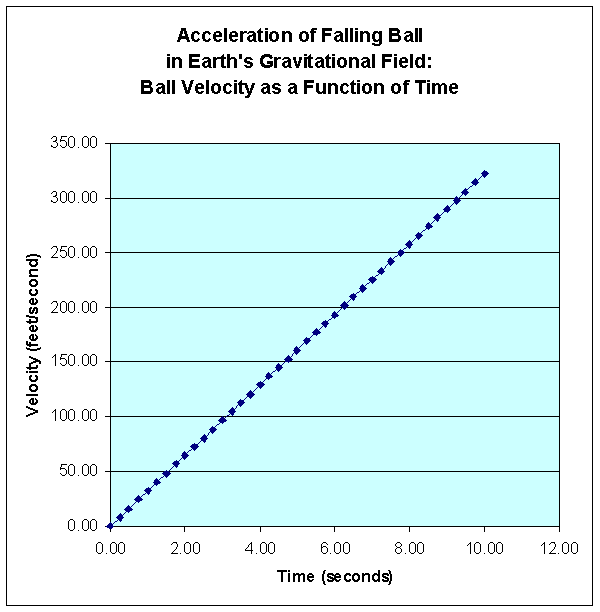 Figure 15: |
||
Let’s consider a photon of light traveling in the vicinity of the Sun’s gravitational field. The Sun’s diameter is 864,000 miles. The Sun’s gravitational field is about 27.8g = 895 feet/second2 acceleration = 0.169 miles/second2 acceleration at the Sun’s surface. A photon of light will travel the Sun’s diameter in 4.64 seconds. A photon of light will be accelerated an additional 0.786 miles/second and Space-Time will be compressed accordingly to keep the measured velocity of light at 186,300 miles/second. Note that this is a gross calculation because the Sun’s gravitational field is only 27.8g at its surface. The Sun’s gravitational field as measured by an observer moving away from the Sun’s is proportional to 1/r2 where r represents the distance of the observer from the center of the Sun. At 432,000 miles above the Sun’s surface, the gravitational field would be 6.95g = 224 feet/second2 acceleration = 0.0424 miles/second2 acceleration. The Sun’s gravitational field is significant enough and large enough to result in measurable bending of the path of a photon of light.
Space-Time Compression can become extremely significant when a massive object is compressed into a small volume making the massive object extremely dense such as is the case with a Neutron Star or Black Hole. The gravitational field near the surface of a Neutron Star is on the order of 2.10 x 1011g = 6.76 x 1011 feet/second2 = 1.28 x 108 miles/second2 = 128,000,000 miles/second2 acceleration. This rate of acceleration is huge compared to the velocity of light at 186,300 miles/second. Such an intense field will very rapidly accelerate a photon, hence, Space-Time Compression occurs very rapidly.
Consider a situation where an observer far from a black hole is watching an astronaut in a spacecraft approach the black hole. The observer would witness time passing extremely slowly for an astronaut falling through the black hole’s Schwartschild radius or event horizon. The distant observer would never actually see the hapless astronaut fall into the black hole. The astronaut’s time, as measured by the observer, would appear to stand still.
Therefore, if a relatively intense gravitational field exists in a localized position in Space-Time relative to an external observer, Space-Time Compression can be measured without objects traveling at velocities very close to the velocity of light relative to the external observer “at rest.”
My Nuclear Gravitation Field Theory determined that the minimum gravitational acceleration field required to overcome the Coulombic Repulsion to be at least 2.441 x 1027g, therefore, the effects of General Relativity must be considered in the vicinity of the nucleus of the atom if the Strong Nuclear Force and gravity are one. Gravity fields propagate based upon Uncompressed Space-Time. In order to “see” or “measure” the Nuclear Gravitation Field propagating outward from the Nucleus omnidirectional in spherical symmetry dropping in intensity 1/r2 consistent with Newton’s Law of Gravity, we would have to measure the field intensity in Uncompressed Space-Time. However, we live in the Compressed Space-Time reference frame, therefore, we see events in Compressed Space-Time. As previously discussed, gravity fields generate the Compressed Space-Time due to the acceleration of light, electric fields, and magnetic fields. Light, Electric Fields, and Magnetic Fields propagate based upon Compressed Space-Time.
Table 2, “Accelerated Reference Frame Space-Time Compression Due to Gravity Field,” below, determines the Uncompressed Space-Time acceleration of light as a function of the intensity of various gravity fields, determines the reduction in the distance traveled by light as observed in Compressed Space-Time, and the resulting Space-Time Compression Factors. Let’s assume the gravitational field next to the nucleus of the atom was equal to 2.9975 x 108 meters/sec2. If light was subjected to this acceleration field, in one second the speed of light would be doubled to 5.9950 x 108 meters/sec equal to the speed of light in Uncompressed Space-Time. Since the speed of light in free space is invariant with respect to the reference frame of the observer, the speed of light remains at 2.9975 x 108 meters/sec. Therefore, the distance traveled by light in Compressed Space-Time must be reduced to half the Uncompressed Space-Time distance as indicated by the first entry highlighted in red in Table 2, “Accelerated Reference Frame Space-Time Compression Due to Gravity Field,” below.
| Gravity Acceleration in g |
Gravity Acceleration (meters/sec2) |
Final Speed of Light in Uncompressed Space-Time After 1 Second (meters/sec) |
Length Reduction Due to Space-Time Compression = cosθ |
arccosθ Radians | arccosθ Degrees | Space-Time Compression Factor = 1/cosθ = secθ |
|---|---|---|---|---|---|---|
| 0 | 0.00 | 2.99750E+08 | 1.00000 | 0.000000 | 0.00000 | 1.00000 |
| 1 | 9.81 | 2.99750E+08 | 1.00000 | 0.000256 | 0.01466 | 1.00000 |
| 2 | 19.62 | 2.99750E+08 | 1.00000 | 0.000362 | 0.02073 | 1.00000 |
| 3 | 29.43 | 2.99750E+08 | 1.00000 | 0.000443 | 0.02539 | 1.00000 |
| 4 | 39.24 | 2.99750E+08 | 1.00000 | 0.000512 | 0.02932 | 1.00000 |
| 5 | 49.05 | 2.99750E+08 | 1.00000 | 0.000572 | 0.03278 | 1.00000 |
| 6 | 58.86 | 2.99750E+08 | 1.00000 | 0.000627 | 0.03591 | 1.00000 |
| 7 | 68.67 | 2.99750E+08 | 1.00000 | 0.000677 | 0.03878 | 1.00000 |
| 8 | 78.48 | 2.99750E+08 | 1.00000 | 0.000724 | 0.04146 | 1.00000 |
| 9 | 88.29 | 2.99750E+08 | 1.00000 | 0.000768 | 0.04398 | 1.00000 |
| 10 | 98.10 | 2.99750E+08 | 1.00000 | 0.000809 | 0.04635 | 1.00000 |
| 20 | 196.20 | 2.99750E+08 | 1.00000 | 0.001144 | 0.06556 | 1.00000 |
| 50 | 490.50 | 2.99750E+08 | 1.00000 | 0.001809 | 0.10365 | 1.00000 |
| 100 | 981 | 2.99751E+08 | 1.00000 | 0.002558 | 0.14659 | 1.00000 |
| 200 | 1962 | 2.99752E+08 | 0.99999 | 0.003618 | 0.20730 | 1.00001 |
| 500 | 4905 | 2.99755E+08 | 0.99998 | 0.005721 | 0.32777 | 1.00002 |
| 1000 | 9810 | 2.99760E+08 | 0.99997 | 0.008090 | 0.46354 | 1.00003 |
| 2000 | 19620 | 2.99770E+08 | 0.99993 | 0.011441 | 0.65553 | 1.00007 |
| 5000 | 49050 | 2.99799E+08 | 0.99984 | 0.018089 | 1.03645 | 1.00016 |
| 10000 | 98100 | 2.99848E+08 | 0.99967 | 0.025581 | 1.46566 | 1.00033 |
| 20000 | 196200 | 2.99946E+08 | 0.99935 | 0.036171 | 2.07247 | 1.00065 |
| 50000 | 49050 | 2.99799E+08 | 0.99984 | 0.018089 | 1.03645 | 1.00016 |
| 100000 | 981000 | 3.00241E+08 | 0.99674 | 0.080794 | 4.62915 | 1.00327 |
| 200000 | 1.96200E+06 | 3.01712E+08 | 0.99350 | 0.114105 | 6.53772 | 1.00655 |
| 500000 | 4.90500E+06 | 3.04655E+08 | 0.98390 | 0.179686 | 10.29526 | 1.01636 |
| 1.000E+06 | 9.81000E+06 | 3.09560E+08 | 0.96831 | 0.1252424 | 14.46283 | 1.03273 |
| 2.000E+06 | 1.96200E+07 | 3.19370E+08 | 0.93857 | 0.352344 | 20.18780 | 1.06545 |
| 5.000E+06 | 4.90500E+07 | 3.48800E+08 | 0.85938 | 0.536750 | 30.75352 | 1.16364 |
| 1.000E+07 | 9.81000E+07 | 3.97850E+08 | 0.75342 | 0.717541 | 41.11209 | 1.32727 |
| 2.000E+07 | 1.96200E+08 | 4.95950E+08 | 0.60440 | 0.921789 | 52.81464 | 1.65455 |
| 3.056E+07 | 2.99750E+08 | 5.99500E+08 | 0.500000 | 1.047198 | 60.0000 | 2.00000 |
| 5.000E+07 | 4.90500E+08 | 7.90250E+08 | 0.37931 | 1.181746 | 67.70903 | 2.63636 |
| 1.000E+08 | 9.81000E+08 | 1.28075E+09 | 0.23404 | 1.334563 | 76.46481 | 4.27273 |
| 2.000E+08 | 1.96200E+09 | 2.26175E+09 | 0.13253 | 1.437875 | 82.38418 | 7.54545 |
| 5.000E+08 | 4.90500E+09 | 5.20475E+09 | 0.05759 | 1.513173 | 86.69842 | 17.36364 |
| 1.000E+09 | 9.81000E+09 | 1.01098E+10 | 0.02965 | 1.541142 | 88.30095 | 33.72727 |
| 2.000E+09 | 1.96200E+10 | 1.99198E+10 | 0.01505 | 1.555748 | 89.13779 | 66.45455 |
| 5.000E+09 | 4.90500E+10 | 4.93498E+10 | 0.00607 | 1.564722 | 89.65198 | 164.63636 |
| 1.000E+10 | 9.81000E+10 | 9.83998E+10 | 0.00305 | 1.567750 | 89.82546 | 328.27273 |
| 2.000E+10 | 1.96200E+11 | 1.96500E+11 | 0.00153 | 1.569271 | 89.91260 | 655.54545 |
| 5.000E+10 | 4.90500E+11 | 4.90800E+11 | 0.00607 | 1.570186 | 89.96501 | 1637.36364 |
| 1.000E+11 | 9.81000E+11 | 9.81300E+11 | 0.00031 | 1.570491 | 89.98250 | 3273.72727 |
| 2.000E+11 | 1.96200E+12 | 1.96230E+12 | 0.00015 | 1.570644 | 89.99125 | 6546.45455 |
| 5.000E+11 | 4.90500E+12 | 4.90530E+12 | 0.00006 | 1.570735 | 89.99650 | 16364.63636 |
| 1.000E+12 | 9.81000E+12 | 9.81030E+12 | 0.00003 | 1.570766 | 89.99825 | 32728.27273 |
| 2.000E+12 | 1.96200E+13 | 1.96203E+13 | 0.00002 | 1.570781 | 89.99912 | 65455.54545 |
| 5.000E+12 | 4.90500E+13 | 4.90503E+13 | 0.00001 | 1.570790 | 89.99965 | 1.63636E+05 |
| 1.000E+13 | 9.81000E+13 | 9.81003E+13 | 0.00000 | 1.570793 | 89.99982 | 3.27274E+05 |
| 2.000E+13 | 1.96200E+14 | 1.96200E+14 | 0.00000 | 1.570795 | 89.99991 | 6.54546E+05 |
| 5.000E+13 | 4.90500E+14 | 4.90500E+14 | 0.00000 | 1.570796 | 89.99996 | 1.63636E+06 |
| 1.000E+14 | 9.81000E+14 | 9.81000E+14 | 0.00000 | 1.570796 | 89.99998 | 3.27273E+06 |
| 2.000E+14 | 1.96200E+15 | 1.96200E+15 | 0.00000 | 1.570796 | 89.99999 | 6.54546E+06 |
| 5.000E+14 | 4.90500E+15 | 4.90500E+15 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+07 |
| 1.000E+15 | 9.81000E+15 | 9.81000E+15 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+07 |
| 2.000E+15 | 1.96200E+16 | 1.96200E+16 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+07 |
| 5.000E+15 | 4.90500E+16 | 4.90500E+16 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+08 |
| 1.000E+16 | 9.81000E+16 | 9.81000E+16 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+08 |
| 2.000E+16 | 1.96200E+17 | 1.96200E+17 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+08 |
| 5.000E+16 | 4.90500E+17 | 4.90500E+17 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+09 |
| 1.000E+17 | 9.81000E+17 | 9.81000E+17 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+09 |
| 2.000E+17 | 1.96200E+18 | 1.96200E+18 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+09 |
| 5.000E+17 | 4.90500E+18 | 4.90500E+18 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+10 |
| 1.000E+18 | 9.81000E+18 | 9.81000E+18 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+10 |
| 2.000E+18 | 1.96200E+19 | 1.96200E+19 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+10 |
| 5.000E+18 | 4.90500E+19 | 4.90500E+19 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+11 |
| 1.000E+19 | 9.81000E+19 | 9.81000E+19 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+11 |
| 2.000E+19 | 1.96200E+20 | 1.96200E+20 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+11 |
| 5.000E+19 | 4.90500E+20 | 4.90500E+20 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+12 |
| 1.000E+20 | 9.81000E+20 | 9.81000E+20 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+12 |
| 2.000E+20 | 1.96200E+21 | 1.96200E+21 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+12 |
| 5.000E+20 | 4.90500E+21 | 4.90500E+21 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+13 |
| 1.000E+21 | 9.81000E+21 | 9.81000E+21 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+13 |
| 2.000E+21 | 1.96200E+22 | 1.96200E+22 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+13 |
| 5.000E+21 | 4.90500E+22 | 4.90500E+22 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+14 |
| 1.000E+22 | 9.81000E+22 | 9.81000E+22 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+14 |
| 2.000E+22 | 1.96200E+23 | 1.96200E+23 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+14 |
| 5.000E+22 | 4.90500E+23 | 4.90500E+23 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+15 |
| 1.000E+23 | 9.81000E+23 | 9.81000E+23 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+15 |
| 2.000E+23 | 1.96200E+24 | 1.96200E+24 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+15 |
| 5.000E+23 | 4.90500E+24 | 4.90500E+24 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+16 |
| 1.000E+24 | 9.81000E+24 | 9.81000E+24 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+16 |
| 2.000E+24 | 1.96200E+25 | 1.96200E+25 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+16 |
| 5.000E+24 | 4.90500E+25 | 4.90500E+25 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+17 |
| 1.000E+25 | 9.81000E+25 | 9.81000E+25 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+17 |
| 2.000E+25 | 1.96200E+26 | 1.96200E+26 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+17 |
| 5.000E+25 | 4.90500E+26 | 4.90500E+26 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+18 |
| 1.000E+26 | 9.81000E+26 | 9.81000E+26 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+18 |
| 2.000E+26 | 1.96200E+27 | 1.96200E+27 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+18 |
| 5.000E+26 | 4.90500E+27 | 4.90500E+27 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+19 |
| 1.000E+27 | 9.81000E+27 | 9.81000E+27 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+19 |
| 2.000E+27 | 1.96200E+28 | 1.96200E+28 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+19 |
| 2.441E+27 | 2.39462E+28 | 2.39462E+28 | 0.00000 | 1.570796 | 90.00000 | 7.98873E+19 |
| 5.000E+27 | 4.90500E+28 | 4.90500E+28 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+20 |
| 1.000E+28 | 9.81000E+28 | 9.81000E+28 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+20 |
| 2.000E+28 | 1.96200E+29 | 1.96200E+29 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+20 |
| 5.000E+28 | 4.90500E+29 | 4.90500E+29 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+21 |
| 1.000E+29 | 9.81000E+29 | 9.81000E+29 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+21 |
| 2.000E+29 | 1.96200E+30 | 1.96200E+30 | 0.00000 | 1.570796 | 90.00000 | 6.54546E+21 |
| 5.000E+29 | 4.90500E+30 | 4.90500E+30 | 0.00000 | 1.570796 | 90.00000 | 1.63636E+22 |
| 1.000E+30 | 9.81000E+30 | 9.81000E+30 | 0.00000 | 1.570796 | 90.00000 | 3.27273E+22 |
From Table 2, “Accelerated Reference Frame Space-Time Compression Due to Gravity Field,” above, we find that the Space-Time Compressed distance that light travels is essentially a zero distance (at five significant digits} for any gravity field acceleration field greater than or equal to
1.00 x 1013g. The minimum gravitational acceleration field required to overcome the Coulombic Repulsion of two protons in a nucleus at
2.441 x 1027g results in Space-Time Compression to a distance of zero because the Space-Time Compression Factor equals 7.99873 x 1019 as indicated by the second entry highlighted in red in Table 2, “Accelerated Reference Frame Space-Time Compression Due to Gravity Field,” above. This is the very reason the Strong Nuclear Force is observed to vanish immediately outside the surface of nucleus of the atom. This observed characteristic of the Strong Nuclear Force can only exist if the Strong Nuclear Force provides an acceleration field to accelerate light. Therefore, the Strong Nuclear Force must be Gravity.
What if intense gravitational fields are not limited to massive stars, neutron stars, and black holes? What if we could amplify a gravitational field locally such that we could develop a Space-Time Compression Factor of 100,000,000 or greater? Recall that a velocity of 0.98c yields a Space-Time Compression Factor of 5.025 and a velocity of 0.999c yields a Space-Time Compression Factor of 22.366 (See Table 1, above). Such compression factors result in reversing the order of events that are only several nanoseconds apart. In addition, it is very impractical to shift from one reference frame to another when one is moving at a velocity close to that of light in one reference frame relative to the other reference frame. With sufficient gravity amplification to obtain a Space-Time Compression Factor of greater than 1017, we could potentially reverse the order of events that occur years apart. It appears that gravity amplification could make interstellar space travel possible and time travel possible.
Conclusion:
General Relativity does make our world and universe seem very strange. Consider two stop watches which are calibrated to operate identically. The first stopwatch is placed in a very strong gravitational field and the second stopwatch is placed in a much weaker gravitational field. Both stopwatches are started at precisely the same instant. The first stopwatch will measure time at a slower rate than the second stopwatch. When both stopwatches are stopped at precisely the same instant, the first stopwatch reading is compared to the second stopwatch reading. The first stopwatch indicates that a shorter interval of time has elapsed between the start and stop of the stopwatches than the interval of time that has elapsed as indicated by the second stopwatch. How can two different time intervals be equal (or the same)? Or, how can the same interval of time be different as measured by two identical clocks? General Relativity!
Space-Time is not linear, it is curved. What appears to be a straight line in space or time may not be because a gravity field is bending the path of light. To an observer, the light path appears to be a straight line. Time appears to be a logical sequence of events. We know that gravity bends or distorts “Space-Time” and light by virtue of the fact that we’re able to see stars which we know should be blocked from our view by our Sun as indicated by Figure 8, above. We’ve used radio and optical telescopes to map stars and other celestial bodies during the course of our yearly orbit around the Sun, so we know where these celestial bodies should be. When the Sun is between us and a background star, many times we can still see that star as though it were in a different position.
Therefore, the apparent location that one observes an object to be may not be its actual location. Don’t trust your eyes, they may deceive you! Likewise, the order of events in Space-Time are dependent upon your reference frame. What may be in your past in one reference frame could, very well, be in your future in an alternate reference frame.
I hope you have appreciated this brief introduction to General Relativity. If you have any comments, please E-Mail the original author, Nymbus, at nymbus@wanadoo.fr or me, Ken Wright, at Info@gravitywarpdrive.com.
![]()
If you are interested in obtaining more information about General Relativity, Space-Time, and Gravitation, you can purchase several books from Amazon.com. You can purchase “Relativity: The Special and General Theory” by Albert Einstein, “An Introduction to General Relativity – Spacetime and Geometry” by Sean M. Carroll, “Gravitation” by Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler, “Relativity – An Introduction to Special and General Relativity” by Hans Stephani, and “Einstein for Dummies” by Carlos I. Calle, PhD.
 |
 |
 |
 |
 |
![]()
HYPERLINKS:
Index and Direct Hyperlinks to the Other Web Pages on this Website:
- Gravity Warp Drive Home Page
- Nuclear Gravitation Field Theory
- History of My Research and Development of the Nuclear Gravitation Field Theory
- “The Zeta Reticuli Incident” by Terence Dickinson
- Supporting Information for the Nuclear Gravitation Field Theory
- Government Scientist Goes Public
- The Physics of Star Trek and Subspace Communication: Science Fiction or Science Fact?
- “Sport Model” Flying Disc Operational Specifications
- Design and Operation of the “Sport Model” Flying Disc Anti-Matter Reactor
- Element 115
- Bob Lazar’s Gravity Generator
- United States Patent Number 3,626,605: “Method and Apparatus for Generating a Secondary Gravitational Force Field”
- United States Patent Number 3,626,606: “Method and Apparatus for Generating a Dynamic Force Field”
- V. V. Roschin and S. M. Godin: “Verification of the Searl Effect”
- Constellation: Reticulum
- Reticulan Extraterrestrial Biological Entity
- Zeta 2 Reticuli: Home System of the Greys?
- UFO Encounter and Time Backs Up
- UFO Testimonies by Astronauts and Cosmonauts and UFO Comments by Presidents and Top U.S. Government Officials
- Pushing the Limits of the Periodic Table
- General Relativity
- Rethinking Relativity
- The Speed of Gravity - What the Experiments Say
- Negative Gravity
- The Bermuda Triangle: Space-Time Warps
- The Wright Brothers
- Favorite Quotes from Famous People
- Sponsors of This Website
- Romans Road to Eternal Life In Jesus Christ
![]()